Problem Statement
A square of side length \(20\) is placed in front of you. You select a point uniformly at random from its interior. Then, independently, a circle of radius \(R \sim \text{Unif}(0,10)\) is formed around the selected point. What is the probability that this circle does not intersect the square at any point?
Original Problem Link: Click here
Solution
Step 1 - Understanding the Core Idea
Let’s build some intuition. Clearly, the best place to pick a point is the center of the square—a circle centered there can grow up to radius \(10\) before touching an edge. Any point away from the center? Well, that’s where things get tricky—closer points to the boundary have a higher chance of their circle spilling out.
Try to visualize the locus of all points that are an equal distance from the closest edge. These points form a smaller concentric square, with perpendicular distance \(x\) from the center. Our goal is now clear:
- Find the probability of choosing a point at a given \(x\).
- Given \(x\), find the probability that a circle centered there does not intersect the square.
- Integrate over all possible \(x\).
Visualizing the Locus
The points that are an equal distance from the nearest edge form a square frame at distance \(x\). Here’s what it looks like:
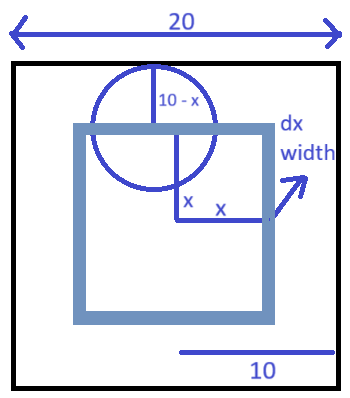
(Yeah ik the diagram kinda sucks, but I believe in MS-Paint XD. Anyhow)
Key observations:
- All points on the same locus are equivalent. The probability of a circle touching the square depends only on \(x\), not on the specific point along the locus.
- Probability of picking a point at distance \(x\):
- The area of the square frame at distance \(x\) is
\(4 \times (2x) \times dx = 8x \, dx\) - Since the total area of the square is \(400\), the probability of selecting a point from this region is
\(\frac{8x \, dx}{400} = \frac{x \, dx}{50}\)
- The area of the square frame at distance \(x\) is
Step 2 - Computing the Probability
Now, assume a point at distance \(x\) has been chosen. What is the probability that a randomly chosen radius does not cause intersection?
- The favorable radii are those that do not exceed \(x\), i.e., \(R \in [0, 10-x]\)
- Since \(R \sim \text{Unif}(0,10)\), the probability that \(R \leq 10 - x\) is simply \(\frac{10 - x}{10}\)
Thus, our probability function is now completely defined. To compute the final probability, we integrate:
\[P(\text{No intersection}) = \int_0^{10} \frac{10-x}{10} \cdot \frac{x}{50} \, dx\]Expanding:
\[P(\text{No intersection}) = \frac{1}{500} \int_0^{10} x(10-x) \, dx\]Breaking it down:
\[\frac{1}{500} \int_0^{10} (10x - x^2) \, dx\]Computing the integral,
\[\frac{1}{500} \left[ 5x^2 - \frac{x^3}{3} \right]_0^{10}\] \[= \frac{1}{500} \left[ 500 - \frac{1000}{3} \right]\] \[= \frac{1}{500} \times \frac{500}{3}\] \[= \frac{1}{3}\]Thus, the probability that the circle does not intersect the square is \(\frac{1}{3}\)
💡 Did you enjoy this problem? Check out more puzzles in the Problems section!